Relationships and graphs

Mathematical functions describe the relationships such as those between pressure and volume or current and voltage. In some cases, the relationship is linear, in others not. All relationship can be described in the form of an equation, where f() represents some mathematical function.

y = f (x)

When plotting a graph, the independent variable (the one which is under experimental control) is assigned to the x-axis, The dependent variable (the value which is being observed or investigated) is assigned to the y-axis. The scales need not include zero and are not necessarily linear - the graph is just an expedient way of picturing a relationship.

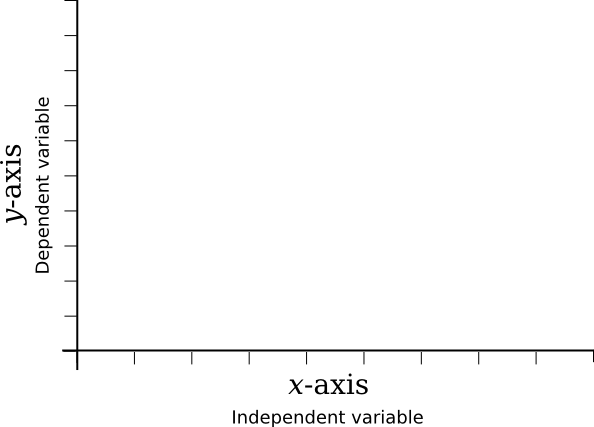
Graph conventions

Linear functions

Linear relationships describe conditions in which the dependent variable changes in proportion with the independent, for example the current through a resistor as the voltage is varied. These equations can be described in the general form of equation 2. Here m represents the gradient of the graph (the rate at which the value of y varies with x ), and c the value of y when x is zero (the y-intercept). The larger the gradient, the faster y increases with any increase in x. The larger the value of c, the greater the value of y when x equals zero (the y-intercept).

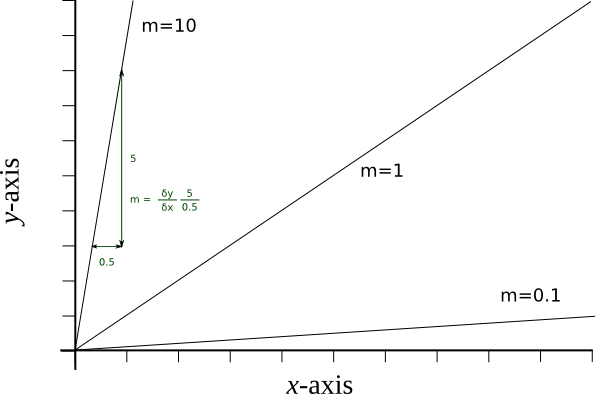
Graphical appearances with differing gradients (m) and constants (c)

Hyperbolic functions

This decribes functions such as equation 3 in which y decreases as x increases (eg. volume with pressure). The magnitude of the relationship is non-linear. When x is small, the are disportionately large changes in the values of y, whereas when x is large, the changes in the value of y are relatively small. Alternatvely, as x increases, y tends towards zero and as x becomes very small, y tends towards ∞.

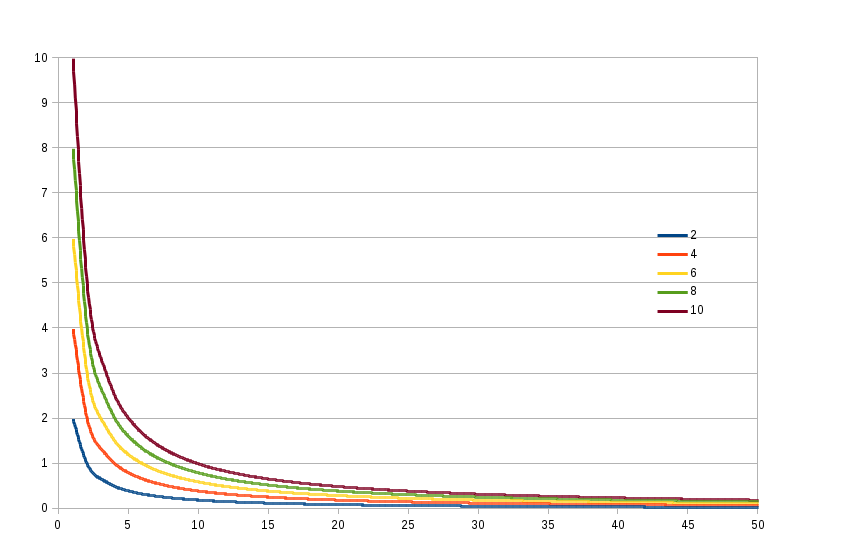
Hyperbolic functions - a family of curves with n = 2 to 10

Powers and bases

Early number systems, such as used by the Romans, exploit symbols which represent specific numbers (I=1, V=5, X=10, L=50 etc. ). These are then combined using a system of addition and subtraction, in order to represent all other numbers ( 12 = XII, 19 = IX ). A far more flexible approach was developed by the Arabic mathematicians in which the position of a digit determines its meaning. This system can be generalised for any number base, as show below.

The value of any digit n in a number, represents n ∗ base^position, where postions left of the decimal point have positive values, and those to the right, negative. Hence the hexadecimal number 0001A (we have to ’invent’ 5 new digits to represent values 10(A), 11(B) ... 15(F) in this number system) represents (0 ∗ 16⁴) + (0 ∗ 16³) + (0 ∗ 16²) + (1 ∗ 16¹) + (A ∗ 16⁰) or 0 + 0 + 0 + 16 + 10 = 26 (rember, any number raised to the power of zero, is 1).

Logarithms

A different way of representing numbers is involves expressing them as a power of the number base. This is represented as log_base . Using base 10, log₁₀ 100 = 2 and log₁₀ 1000 = 3. With the use of fractional exponents, any rational number can be represented, for example log₁₀1923.45 = 3.284 (10^3.284).

Two number bases are in common use, base 10 and base e, which has an approximate value of 2.718.

Logarithms to base e are often referred to a natural logarithms and represented by ln, rather than log_e.

Traditionally, logarithms have been used as a means of simplifying difficult calculations. Before calculators, large multiplactions and divisions were time consuming and error prone. Logarithms help, because they have useful properties as show in Box 1. Tables of logarithms were published in books. For more informatione see (rapid-tables and chilimath

Exponential functions

Exponential functions take the form b_n, where 'b' is the base and 'n' is termed the exponent. Just like logs, these functions have their own rules (more at chilimath.

Euler's number 'e'

The logs sections referred to log to the base 'e' and you will see this value cropping up in many equations. 'e' is a fundamental constant and an irrational number (like π, its calculated value is of unlimited length) with an approximate value of 2.7183. e was first described by Bernoulli when investigation the effects of compound interest ! The Wikipedia description is worth reading. As the compounding frequency is increased (annual, monthly, weekly, daily etc), the value of the investment increases, but the rate of increase tails off towards a maximum value. £1 invested for 1 year at in interest rate of 100% with ∞ compounding frequency would return £2.718...

In more general terms:

N_t = N₀ * e^{rate constant * t}

where N₀ is the number at the start of the period (t=0) and N_t is the number at the end of the period (t) i.e. the final quantity.

The rate constant (k) is the ratio of N_t/N₀ per time period - i.e. if the we see a doubling in size in one time period, then N_t/N₀ = 2 and the value of the rate constant k must be ln 2 (2=e^k, so k=ln2)

So far, pretty abstract as this is based on '∞ compounding frequency of interest' (very nice, I'm sure..). However, if we replace those words with 'continuous growth', then the application becomes a little more obvious.

If a bacterial colony doubles in size hourly (continuous growth), then after 5 hours (5*t), what will a colony of 100 bacteria developed into ?

When you see 'e' popping up in equations, you are likely to be dealing with process of continuous growth (or its inverse), such as radioactive decay, charging or discharging of capacitors

For a very good review of mathematical relationships in anaesthesia and critical care, see this BJA CEACCP article.