Pressure is force per unit of area i.e. P=F/A. Without this standardization, it is difficult to understand the implications of any force (Fig. 1)
One of the simplest ways in which to measure pressure, is through the use of a liquid column or manometer (Fig. 2). When a positive pressure (P) is applied to the right limb, it pushes the fluid level down until an equilibrium is achieved. At equilibrium, the mass of the fluid column, h*A*ρ (where A is the cross-secionial area of the fluid column and ρ, the density of the fluid) exerts exactly the same force as that applied to the surface of the fluid on the right limb. Using F=ma and P=F/A, hAρg/A = P. Since the density of the fluid and cross-sectional areas are constants, this simplifies to P ∝ h and pressure measured in this way is often expressed in terms of the fluid column height (cmH2O or mmHg).
Changing the fluid (i.e. using fluids of different denisties) allows manometer tubes of the same length to measure very different pressures. Mercury is 13.5 times more dense than water, so using a mercury filled manometer would allow readings of pressures 13.5 the magnitude of the same column of water. Altering the cross-sectional area of the tube has no effect as can be seen from the above equation where A features in both the numerator and denominator and disappears from the calculation.
At first thought, it would seem attractive to measure pressure with reference to an absolute zero point (vacuum) as we do temperature (Kelvin). In practice, this is of limitted use and is seldom used other than for mesurement of atmospheric pressure.
The mercury barometer uses a glass tube, closed at one end and completely filled with mercury. The open end is placed in a beaker of mercury and raised to a vertical position, such that no air enters the tube (Fig. 3).
Mercury is very dense (13534 kgm-3 and so even a short column has considerable mass i.e. height (h) * cross-sectional area (A) multiplied by its density (ρ). As a result, the mercury column will fall, creating a vaccum above it, until an equilibrium is reached with the pressure of the mercury column being balanced by atmospheric pressure acting on the mercury in the open beaker.
P = F/A [1]
Where P=Pressure, F=Force and A=area
F = ma [2]
Where F=Force, m=mass and a=acceleration
m = vρ [3]
Where m=mass, v=volue and ρ=density
v = hA [4]
v=column volume, h=column height and A=cross-sectional area
In [2], a = acceleration due to gravity or N (9.8ms2)
So, from [1,2,&3]
P = (hAρ)N/A or Nhρ [5]
BUT P = 1 atmosphere, so from [5]
1 atmosphere = (Nρ)h
Atmospheric pressure ∝ h mmHg
If Patmos = 101kPa, h=0.76m expressed as 760mmHg
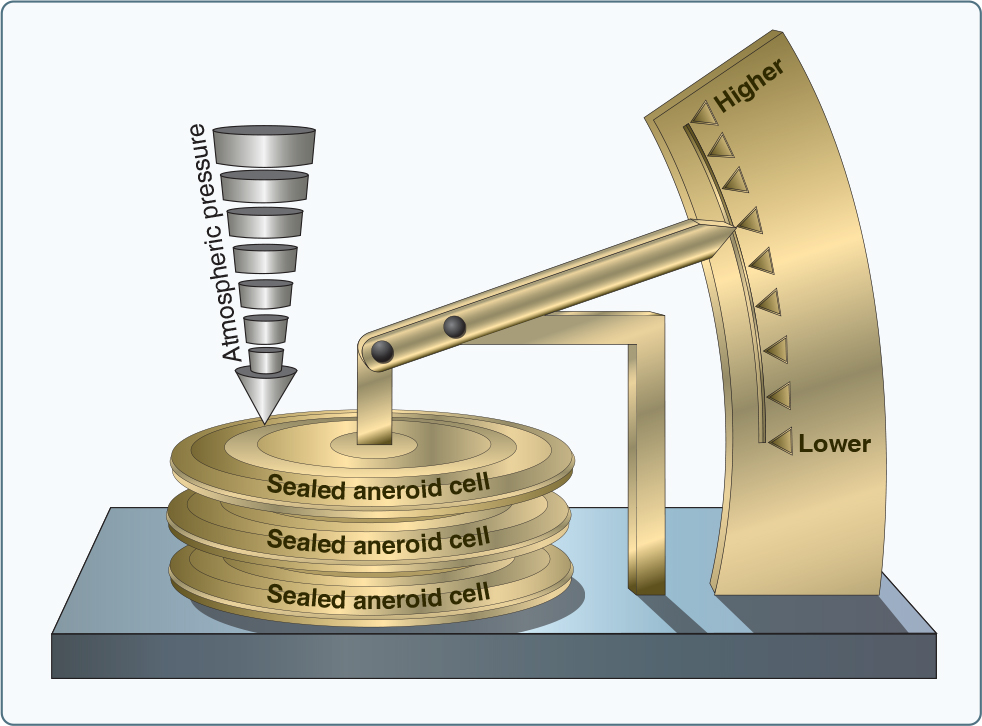
Since there is a vacuum above the mercury in the tube, the barometer is providing an absolute pressure measurement i.e. pressure above zero, but at the cost of a cumbersome, fragile apparatus filled with a toxic liquid. A more portable solution is the anaeroid barometer in which an evacuated bellows is used (Fig. 4). This is now a delicate mechanism which requires careful calibration and which is wholly dependent on maintaining the vacuum within the anaeroid cells.
For clinical purposes, it is generally more useful to measure pressure relative to atmospheric pressure; an oxygen cylinder which has an absolute pressure of 1 atmosphere is of no use at all as no gas will flow out of it (there is no pressure gradient). Far more useful is a relative pressure gauge (which will show zero or empty) when connected to the same cylinder (Fig. 5). This is referred to as 'gauge pressure'.
| Unit | Symbol | Definition | Equivalence |
|---|---|---|---|
| Pascal | Pa | 1Nm-2 | 1 atm = 101325 Pa |
| Torr | Torr | 1mmHg | 1 atm = 760 Torr |
| Pounds per square inch | psi / lb/in.2 | 1 atm = 14.7 psi 137 bar ≈ 2000psi |
|
| Bar | bar | 100kPa | 1 atm = 1.01325 bar |
Although manometers are still used in clinical practice (measurement of CSF pressure), it is realtively unusual to see them. Other types of pressure measuring devices are much more common.
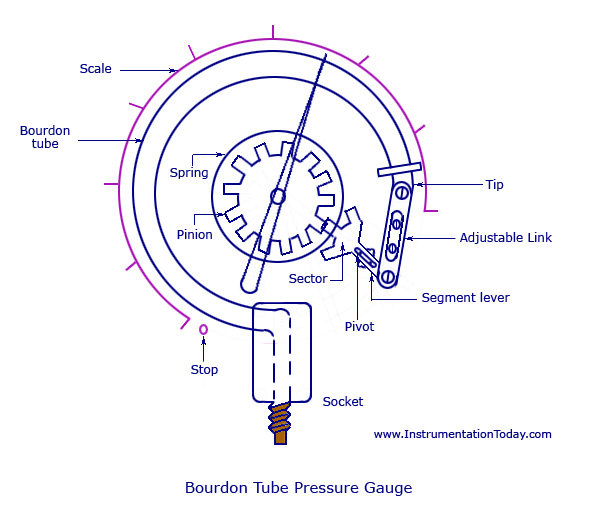
The Bourdon gauge consists of a curved or coiled metal tube. Rising pressure within the tube tends to straighten it and this is used to move a pointer (Fig.6). The Bourdon guage has the advantage of being robust and durable and is used on the anaesthetic machine to indicate the pressures in the gas pipelines.
These devices convert a mechanical signal into an electrical. Perhaps the mostobvious of these which we handle is the arterial pressure transducer, the most common variety of which uses a sensor which responds to changes in pressure; this is a strain gaug and it changes its electrical resistance in response to mechanical strain or pressure.
The strain gauge is often placed on a flexible diaphragm which deforms in response to changes in arterial pressure. As this happens, it causes a change in the resistance of the strain gauge. These changes are tiny and any measurement device must not disturb the properties of the system. Fortunately, you already know of a system designed for this purpose - the Wheatstone bridge.
A modern pressure transducer with details inset. Transducer in fluid chanel (top-left) and the electronics with the rear case removed(top-right).
Each transducer will be a little different. As a result, it must be calibrated or 'zeroed' before use. This easiest reference pressure is atomspheric, so the transducer is exposed to this ('Off to patient, open to air'). This step has nothing to do with the patient and can be done with the patient-end of the line disconnected and with the transducer at any height. Once the zero is completed, the monitor is able to convert the signal it receives into a representation of the pressure which the transucer is sensing. For this to mean anything, the transducer MUST be placed at level we wish to interpret as 0. For a blood pressure measurement, this is the level of the atrium (although in neurosurgery we may choose to measure pressure from the level of the tragus - the monitors will display numbers, but it is up to us to interpret them in a sensible way.